Chap.I 理論基礎

Part 4：統計 & 機率

Analyze the data through data visualization using Seaborn

https://reurl.cc/ZGgbQ6

2. Statistics Fundamentals 基礎統計

import pandas as pd
df = pd.DataFrame({
    'Name': ['Dan', 'Joann', 'Pedro', 'Rosie', 'Ethan', 'Vicky', 'Frederic'],
    'Salary':[50000, 54000, 50000, 189000, 55000, 40000, 59000],
    'Hours':[41, 40, 36, 30, 35, 39, 40],
    'Grade':[50, 50, 46, 95, 50, 5, 57]
    })

2-1. Descriptive Statistics 敘述統計量

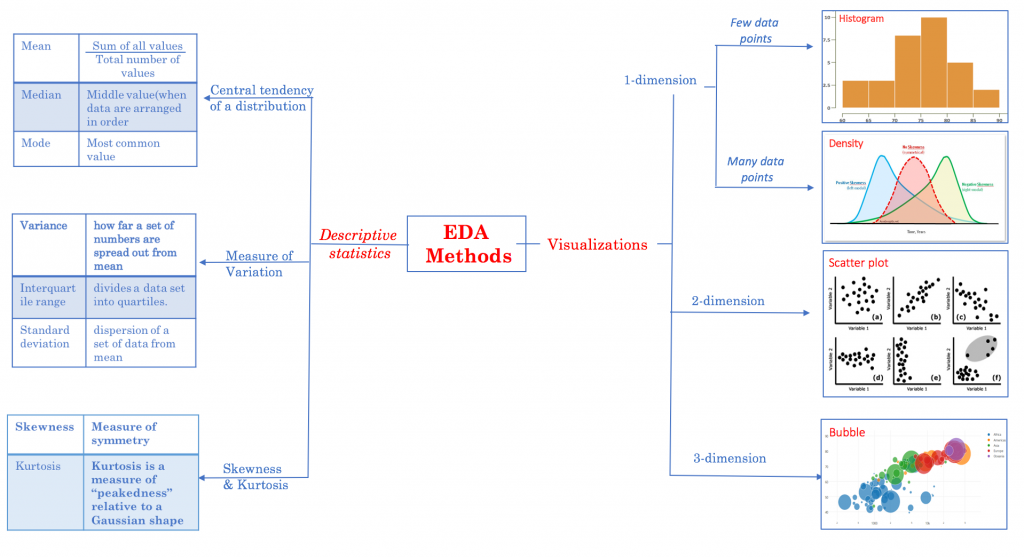
統計學中，描繪或總結觀察量的基本狀態的統計總稱為描述統計量。

A. 數值的描述統計量：

pd.set_option('precision', 2)   # 顯示兩位數

print(df.describe())
>>            Salary  Hours  Grade
    count       7.00   7.00   7.00
    mean    71000.00  37.29  50.43
    std     52370.48   3.90  26.18
    min     40000.00  30.00   5.00
    25%     50000.00  35.50  48.00
    50%     54000.00  39.00  50.00
    75%     57000.00  40.00  53.50
    max    189000.00  41.00  95.00

B. 文字類型的描述統計量：

print(df.describe(include='O'))
>>          Name
    count       7   # 計數
    unique      7   # 不同類型的資料數
    top     Vicky   # 最上方資料
    freq        1   # 重複頻率最高次數

C. Mean 平均數

為總數的平均。平均數容易因為極值導致失去準確性。

print(df['Salary'].mean())

>>  71000.0

D. Median 中位數

所有數據位於正中間的那個。相對平均數，中位數較不易因極端值導致預測失準。

print(df['Salary'].median())

>>  54000.0

E. Mode 眾數

即投票，票多者勝。

print (df['Salary'].mode())

>>  0    50000
    dtype: int64

2-2. Distribution and Density 分配與密度

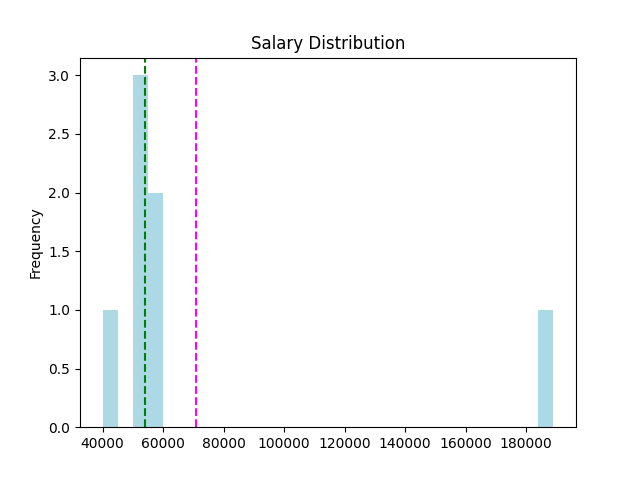
一樣使用上一個 DataFrame，我們將它畫成直方圖 (Histogram)

import matplotlib.pyplot as plt

# n: 每個級距中資料的個數，共 25 級距
# x: 級距的邊緣，共 26 個 (含頭尾)
# _: matplotlib 物件名稱
S = df['Salary']
n, x, _ = plt.hist(S, histtype='step', bins=25, color='lightblue')

plt.axvline(S.mean(), c='m', linestyle='--')     # 平均
plt.axvline(S.median(), c='g', linestyle='--')   # 中位數

plt.show()

發現資料分布是一個 right-skewed 右偏態，極值將平均向右拉扯。

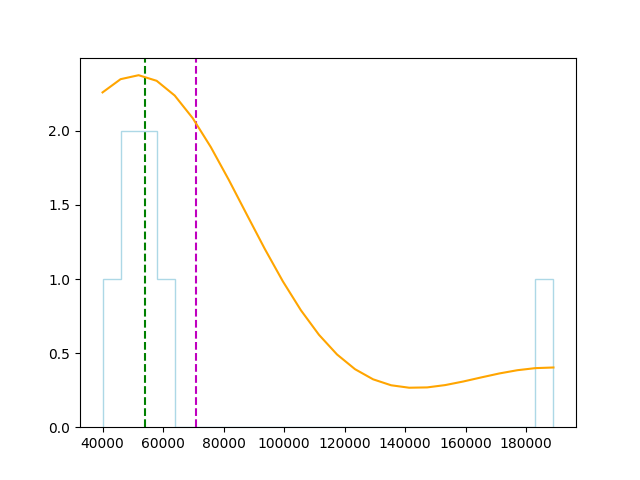
可以使用 pandas 指令來呈現偏態：

density = stats.gaussian_kde(S)
plt.plot(x, density(x)*250000, c='orange')

plt.show()

偏度與峰度：

print('Skewness: ' + str(S.skew()))
print('kurtosis: ' + str(S.kurt()))
>>  Skewness: 2.57316410755049    # 偏度
    Kurtosis: 6.719828837773431   # 峰度

2-3. Measures of Variance 變異數的衡量

A. Range (max-min)

numcols = ['Salary', 'Hours', 'Grade']
for col in numcols:
     print(df[col].name + ' range: ' + str(df[col].max() - df[col].min()))

>>  Salary range: 149000
    Hours range: 11
    Grade range: 90

B. Percentiles 百分位數

strict: 表示小於這個值的百分位數。
weak: 表示小於或等於這個值的百分位數。
rank: 表示碰到相同值，他們共享這個百分位數。

method = ['strict', 'weak', 'rank']
for i in method:
    a = pr(df['Grade'], df.loc[6, 'Grade'], i)
    print(f'Grade ({i}): {a:.2f}')
    
>>  Grade (strict): 71.43
    Grade (weak): 85.71
    Grade (rank): 85.71

C. Quartiles 四分位數

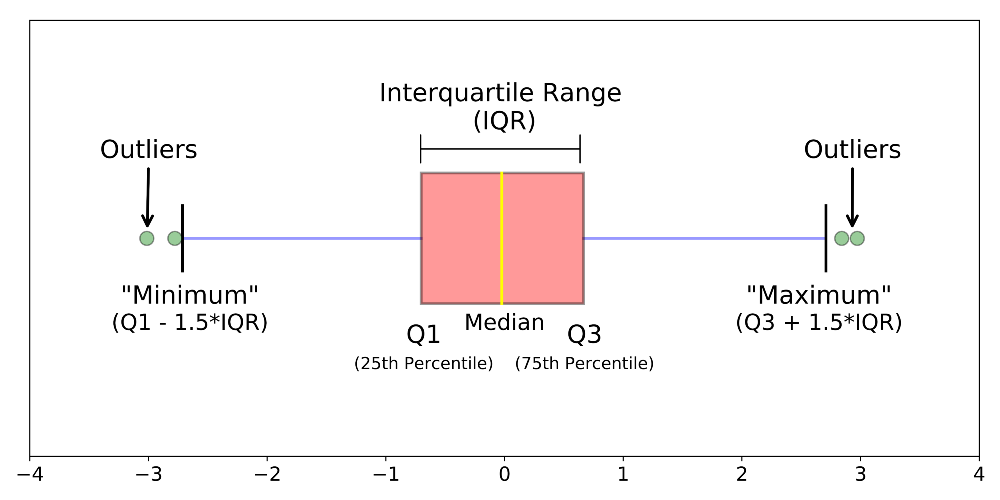
Box plot可以觀察以下

1. 左右兩側為最大（Q3+1.5IQR）與最小值（Q1-1.5IQR）
2. 中間線段為中位數
3. 盒子兩側為Q1（25% Percentiles）、Q3（75% Percentiles）
   

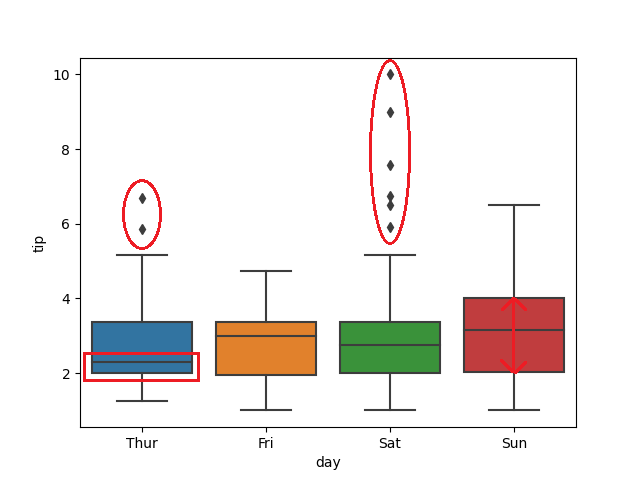
使用 seaborn 中的內建資料集 'tips' 來分析：

import seaborn as sns
import matplotlib.pyplot as plt

df2 = sns.load_dataset('tips')

sns.boxplot('day', 'tip', data=df2)
plt.show()

1. 週四的平均值比週五、週六、週日少（紅框）
2. 週六的離群值多出許多（紅圈）
3. 週日的小費上下區間差異最大（箭頭）

D. Variance and Standard Deviation 變異數與標準差

D-1. Variance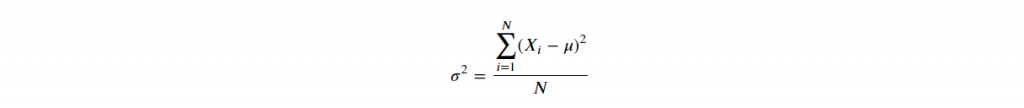

# 1. pandas 預設為樣本變異數，ddof=1，即分母為 N-1
df['Grade'].var()

>>  685.6190476190476

# 2. numpy 預設為母體變異數，ddof=0，即分母為 N
np.var(np.array(df['Grade']))

>>  587.6734693877551

D-2. Standard Deviation
由於變異數為求距離為正數，作了平方和，導致與實際值相差甚遠，
因此，變異數再開根號，使規模相符，稱之為標準差。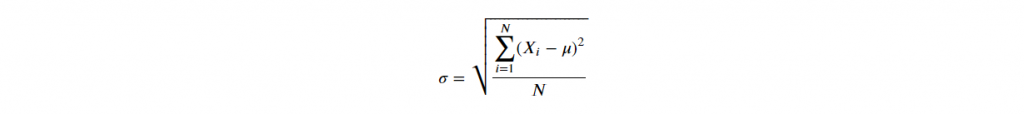

# 1. pandas 預設為樣本標準差，ddof=1，即分母為 N-1
df['Grade'].std()

>>  26.184328282754315

# 2. numpy 預設為母體標準差，ddof=0，即分母為 N
np.std(np.array(df['Grade']))

>>  24.24197742321684

3. Comparing Data 資料比較

3-1. 變數類型

A. Univariate Data 單變數

以上述例子為例，若資料僅包含薪資待遇，則為一個單變數資料。
常利用箱型圖、直方圖分析特性。

df = pd.DataFrame({
    'Name': ['Dan', 'Joann', 'Pedro', 'Rosie', 'Ethan', 'Vicky', 'Frederic'],
    'Salary':[50000, 54000, 50000, 189000, 55000, 40000, 59000],
    })

B. Bivariate or Multivariate Data 雙變數或多變數

常利用散布圖、多個箱型圖分析特性。

df = pd.DataFrame({
    'Name': ['Dan', 'Joann', 'Pedro', 'Rosie', 'Ethan', 'Vicky', 'Frederic'],
    'Salary':[50000, 54000, 50000, 189000, 55000, 40000, 59000],
    'Hours':[41, 40, 36, 30, 35, 39, 40],
    'Grade':[50, 50, 46, 95, 50, 5, 57]
    })

3-2. Feature Scaling 特徵縮放

1. 使特徵規模一致，求解收斂速度快
2. 提高準確率
   通常有以下兩種方式：

A. Standard Score (Z-score) 標準化

藉由從單一（原始）分數中減去母體的平均值，再依照母體（母集合）的標準差分割成不同的差距。
白話文： x 與平均數之間相隔多少個標準差。

from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
df[['Salary', 'Hours', 'Grade']] = scaler.fit_transform(df[['Salary', 'Hours', 'Grade']])
print(df)
>>         Name  Salary  Hours  Grade
    0       Dan   -0.43   1.03  -0.02
    1     Joann   -0.35   0.75  -0.02
    2     Pedro   -0.43  -0.36  -0.18
    3     Rosie    2.43  -2.02   1.84
    4     Ethan   -0.33  -0.63  -0.02
    5     Vicky   -0.64   0.47  -1.87
    6  Frederic   -0.25   0.75   0.27

B. Normalizing 歸一化

重新縮放特徵的範圍到[0, 1]或[-1, 1]。
白話文： x 在 max 和 min 中等比例的位置。

from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
df[['Salary', 'Hours', 'Grade']] = scaler.fit_transform(df[['Salary', 'Hours', 'Grade']])
print(df)
>>         Name  Salary  Hours  Grade
    0       Dan    0.07   1.00   0.50
    1     Joann    0.09   0.91   0.50
    2     Pedro    0.07   0.55   0.46
    3     Rosie    1.00   0.00   1.00
    4     Ethan    0.10   0.45   0.50
    5     Vicky    0.00   0.82   0.00
    6  Frederic    0.13   0.91   0.58

歸一化的資料在小型計算上並不會體現差異，

但若演算龐大數據，利用歸一化後的資料 scale 小，其收斂速度較快。

import matplotlib.pyplot as plt
df.plot(kind='scatter', title='Grade vs Salary', x='Grade', y='Salary')
plt.show()

3-3. Pairplot 配對圖

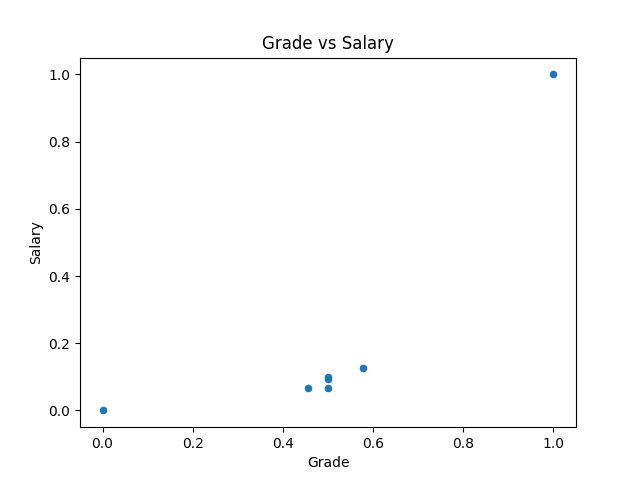
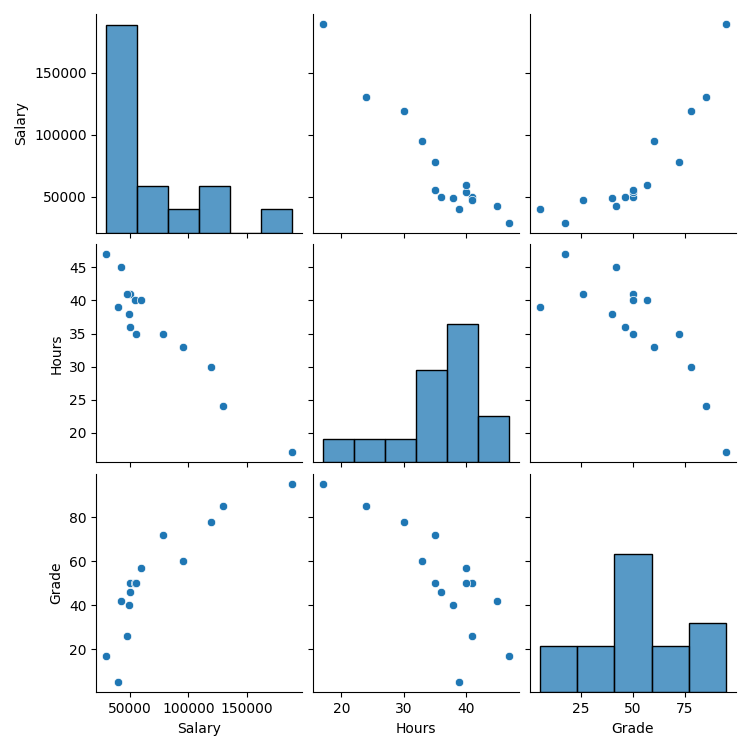
在 seaborn 中，可以用 pairplot 指令畫出所有變數對應的散布圖。
3個變數 → 得到 3*3 張圖
首先我們把更大量的資料丟進python

df = pd.DataFrame({
    'Name': ['Dan', 'Joann', 'Pedro', 'Rosie', 'Ethan', 'Vicky', 'Frederic', 'Jimmie', 'Rhonda', 'Giovanni', 'Francesca', 'Rajab', 'Naiyana', 'Kian', 'Jenny'],
    'Salary':[50000,54000,50000,189000,55000,40000,59000,42000,47000,78000,119000,95000,49000,29000,130000],
    'Hours':[41,40,36,17,35,39,40,45,41,35,30,33,38,47,24],
    'Grade':[50,50,46,95,50,5,57,42,26,72,78,60,40,17,85]
    })

接著

import seaborn as sns
import matplotlib.pyplot as plt
sns.pairplot(df)

plt.show()

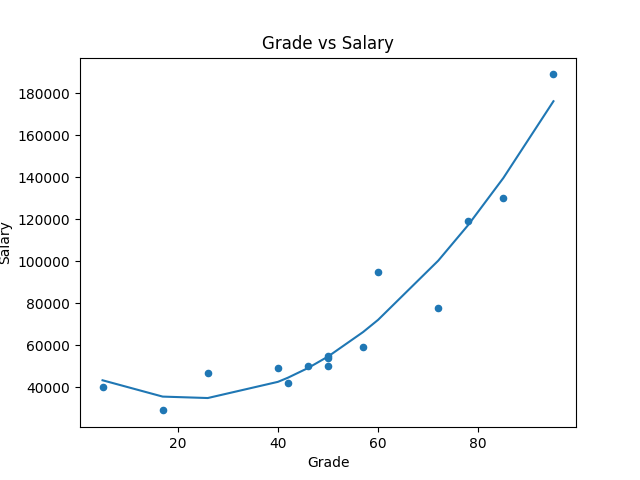
進一步使用 numpy 內建的 poly1d, polyfit 來做線性迴歸：

df.plot(kind='scatter', title='Grade vs Salary', x='Grade', y='Salary')

# 先求出迴歸線
reg = np.polyfit(df['Grade'], df['Salary'], 2)

# 定義 x 與 y
x = np.unique(df['Grade'])  # 去除重複數字
y = np.poly1d(reg)(x)       # 帶入迴歸線涵式

plt.plot(x, y)

3-4. Correlation 關聯性

用數字表示兩個不同資料間，存依關係大小，稱關聯性。
公式如下：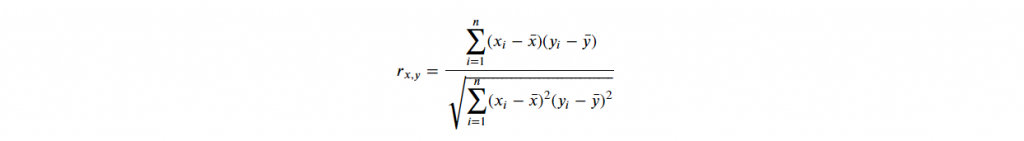

其值會介於 -1~1 間（正相關與反相關），其絕對值越靠近 1 表示關聯性越大。
一般而言，超過 0.8 即高度相關。

print(df.corr())   # 自己與自己必定全關聯

>>          Salary  Hours  Grade
    Salary    1.00  -0.95   0.86
    Hours    -0.95   1.00  -0.81
    Grade     0.86  -0.81   1.00

如果將其視覺化，可運用 seaborn 熱力圖：

import seaborn as sns
import matplotlib.pyplot as plt

sns.heatmap(np.abs(df.corr()))   # 取絕對值才能看出相關
plt.show()

4. Probability 機率

4-1. Basic

．Experiment 實驗：
表示一具有不確定結果的動作。如：拋硬幣。
．Sample space 樣本空間：
實驗所有可能結果的集合。拋硬幣中，有一組兩種可能的結果（正和反）。
．Sample point 樣本點：
是單個可能的結果。如：正面
．Event 事件：
某次實驗發生的結果。如：正面
．Probability 機率：
某種事件發生的可能性。如：正面機率為 50%
事件發生機率 = 某事件的樣本點/樣本空間所有樣本點

EX.1 若丟兩次骰，總和為7的機率為?

1. Sample space = 6*6 = 36
2. Sample point = 6
3. Probability = 6/36 = 16.7%

EX.2 若丟兩次骰，總和大於4的機率為?
(此例用反面機率計算較快)
計算總和小於等於4

1. Sample space = 6*6 = 36
2. Sample point = 6
3. P(A) = 1 - 0.167 = 83.3%

4-2. Conditional Probability and Dependence 條件機率與相依性

A. Independent Events 獨立事件

EX. 丟硬幣
第一次丟正面，並不影響第二次丟正面的機率。

import random

# 創建一個 list 代表正面與反面
heads_tails = [0, 0]

# 重複丟一萬次
trial = 0
while trial < 10000:
    trial += 1
    toss = random.randint(0,1)
    heads_tails[toss] += 1
print (heads_tails)
>> [5050, 4950]

# 作成 pie chart
from matplotlib import pyplot as plt
plt.figure(figsize=(5,5))
plt.pie(heads_tails, labels=['heads', 'tails'])
plt.legend()

plt.show()

B. Dependent Events 相依事件

第一事件的結果會影響第二事件。
如抽撲克牌（且不放回）兩張，其中一張為紅的機率為何：
(26/52) * (26/51) = 25.49%

C. Mutually Exclusive Events 互斥事件

事件 A 與 事件 B 同時發生的機率為　0，即 ?(?^?)=0，
如丟骰，丟到 6 點，及丟到奇數，為互斥事件。

4-3. Variables and Distributions 二項變數與分配

．Bernoulli 白努力分配：
作一次二分類的實驗。如：拋 1 次硬幣。
．Binomial 二項分配：
作多次二分類的實驗。
．Multinomial 多項分配：
作多次多分類的實驗。如：丟多次骰。

A. Permutation 排列

須講究＂順序＂的取用方式。以下為程式碼：

# 3 取 2 排列
from itertools import permutations 

perm = permutations([1, 2, 3], 2) 
for i in list(perm):
    print (i)
>>  (1, 2)
    (1, 3)
    (2, 1)
    (2, 3)
    (3, 1)
    (3, 2)

print(len(list(perm)))

>>  6

B. Combination 組合

不講究順序，僅在乎取用物件。以下為程式碼：

from itertools import combinations

comb = combinations([1, 2, 3], 2)

for i in list(comb): 
    print(i)

>>  (1, 2)
    (1, 3)
    (2, 3)

C. Allowing for Bias 允許偏差（機率不相等）

EX1. 重複丟硬幣3次，丟出各組合的機率為何?（正面機率為40% 反面為60%）

from scipy.stats import binom
import matplotlib.pyplot as plt
import numpy as np

trials = 3
p = 0.5
x = np.array(range(0, trials+1))

prob = [binom.pmf(k, trials, p) for k in x]

# 作圖
plt.xlabel('Successes')
plt.ylabel('Probability')
plt.bar(x, prob)
plt.show()

EX2. 我們拿最近很夯的丁特抽天堂 M 紫布來看看...

n = 475 # 總共抽卡475次
p = 0.1 # 抽卡中獎機率 10%
x = np.array(range(0, n+1)) # 中獎次數

P = [binom.pmf(k, n, p) for k in x]

plt.xlabel('x')
plt.ylabel('Prob')
plt.bar(x, P)   # 把中獎次數作 x 軸，發生此事件的機率作 y 軸
plt.axvline(11, c='r', linestyle='--', linewidth=2)

print('丁特抽卡475次，機率10%情況，只中11次的機率為: ', f'{binom.pmf(11, n, p)}')
>> 丁特抽卡475次，機率10%情況，只中11次的機率為:  3.633598716610176e-11
plt.show()

從圖中可以發現，最有可能出現的次數為 47.5 次，根據基礎統計來看...

橘子公司內部調整的紫布機率肯定不會是10%!!!

1. mean = n*p = 475 * 0.1 = 47.5
2. var = n * p * (1-p)
3. std = (n * p * (1-p)) ^ 0.5

4-4. Binomial Distribution Expected Value & Variance 二項分配的期望值與變異數

A. Expected Value 期望值

B. Variance 變異數

C. Standard Deviation 標準差

.
.
.
.
.

Homework：

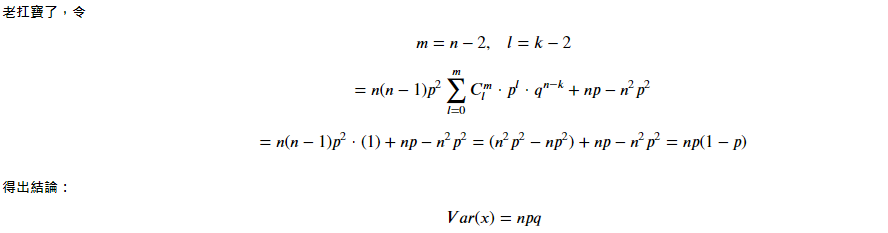
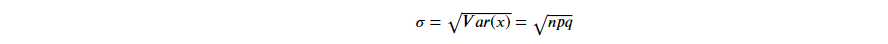
#1. 今彩 539

1. 請問各個獎項中獎機率為?
2. 請問每張彩券平均報酬率?

https://www.taiwanlottery.com.tw/dailycash/index.asp

須從 01~39 的號碼中任選5個號碼進行投注。
開獎時，開獎單位將隨機開出五個號碼，這一組號碼就是該期今彩539的中獎號碼，也稱為「獎號」。
五個選號中，如有二個以上（含）對中當期開出之五個號碼，即為中獎，並可依規定兌領獎金。
各獎項的中獎方式如下表：

獎金如下：

#2. 使用 sklearn 內建資料集 "load_boston" 來預測波士頓房價
提示：

1. Data prepare 準備資料
2. Data clean 資料清理
3. Feature Engineering 特徵工程
4. Split 拆分資料
5. Train Model 機器訓練
6. Score Model 為模型打分
   .
   .
   .
   .
   .

補充：線性迴歸

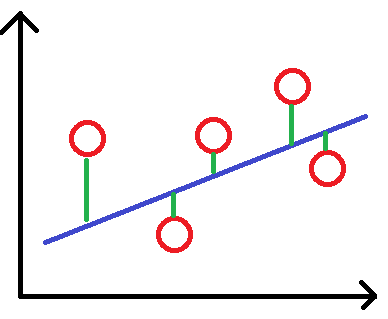
假設有一資料如下圖，紅點為資料，藍線為其迴歸線